D-Efficiency In Depth
D-Efficiency
D-efficiency summarizes how precisely this design can estimate all the parameters of interest with respect to another design, rather than how well the design can estimate the utility of each level of each attribute (as with the simpler default test). D-efficiency is described in an article by Kuhfeld, Tobias, and Garratt (1994), "Efficient Experimental Design with Marketing Research Applications," Journal of Marketing Research, 31 (November), 545-557.
To arrive at D-efficiency, we should define a few terms:
| Xt | = design matrix for task t with a row for each alternative |
| xi | = ith row of Xt |
| pi | = probability of choice of alternative i |
| v | = probability-weighted means of rows: v = 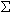 i pi xi i pi xi |
| Zt | = matrix with ith row zi = pi1/2 ( xi - v) |
| Z | = matrix made by appending all Zt matrices |
Z'Z is known as the "Information Matrix"
The determinant of Z'Z measures the strength of the design.
Because the magnitude of the determinant of Z'Z depends on the number of parameters estimated, to provide a measure of strength independent of p we consider the pth root of the determinant:
|Z'Z|1/p
Where Z is the probability-centered design matrix, Z'Z is the "Information Matrix," and p is the number of parameters estimated.
The pth root of the determinant doesn't result in a single value bounded by 0 and 1.0 (as with the simpler test efficiency report), and this value is meaningless without reference to the same computed for comparison design. This value also depends on the number of respondents x tasks, so when comparing two designs, it is important to hold the number of respondents x tasks constant. We use the term "efficiency" to compare the relative strengths of two designs. The relative D-efficiency of one design with respect to the other is given by the ratio of the pth root of the determinants of their information matrices. The design with a larger value is the more efficient design. (Note: we only consider the precision of parameters other than the "None" parameter when computing the strength of the design.)
Consider design A with no prohibitions and design A' with prohibitions. The pth root of the determinant of the information matrix is computed for both (holding the number of respondents, tasks, concepts per task, and None % constant). If design A' has a value of 2,500 and design A has a value of 3,000, design A' is 2,500/3,000 = 83.3% as efficient as design A. The inclusion of prohibitions resulted in a 1 - 0.833 = 16.7% loss in efficiency.